Reasoning about design

Most engineering disciplines have some way to model the system that is being built and to reason about the design of the system before it is constructed. That does not mean that no testing is performed, for models are but approximations of the real thing and could be wrong! For example, see this video of a boeing wing test and as the test is performed and the wings fail, you can see the engineers smiling and cheering. Why? because it proved that their model. In fact having sufficient testing can have disastrous effects, as was shown in the construction and collapse of the Tacoma Narrows Bridge.

Software construction on the other hand, follows more closely this model from Calvin and Hobbes. The only validation most of us do is using testing. The problem with testing, is that in the presence of multi-threading and concurrency, it might not be possible to simulate all the possible executions paths, leading to Heisenbug’s that might be difficult to track down or even not be known till they occur in production.

As we all know, and as was reported in this paper , the relative cost of fixing a bug raises nearly exponentially the later it is found in the lifecycle, and being found in production is the worst.

So the question arises, is there a way to test the “design” of software systems, before we write code, so that we can be sure that the design itself does not have flaws? It’s important to note that, design bugs, like protocol flaws between systems that can lead to data corruption, would by definition, be close to impossible to fix using code, without changing the design itself.

Leslie Lamport won the turing award in 2013 for inventing and building a system to be able to model software systems and then check these models, especially, those of concurrent and distributed nature. This system

This system is known as TLA, which stands for Temporal Logic of Actions, as described here

… has become a shorthand for referring to the TLA+ specification language and the PlusCal algorithm language, together with their associated tools.

The TLA⁺ Hyperbook goes over the details of using this specification using The Standard Model. The Standard Model is defined in the book as

The Standard Model As abstract system is defined as a collection of behaviors, each representing a possible execution of the system, where a behavior is a sequence of states and a state is an assignment of values to variables.

The specification uses formal mathematics to define the steps (assignment of values) and transitions from one state to the next. Luckily for us programmers and practitioners who might not be as comfortably versed in terms of thinking in terms of boolean logic and sets, there is also the PlusCal language, where one can describe the system in more familar code like semantics which then automatically get translated into the mathematical spec. This spec can then be validated by creating a model and run it to check for constraints.

Constraints in this case is some mathematical definition of some property that needs to hold true if the system being modeled is deemed to be correct.

Hello World

To make it more concrete, let’s start with a simple example. The complete example is here.

--algorithm HelloWorld
variables n = 0;
begin
    n := n + 1;
end algorithm;

This code describes a simple specification, using pluscal, having a variable n whose intial value is zero. When the spec run, the only thing it does is add 1 to it. This describes the “what” of the specification.

The translated code in TLA, looks as follows:

VARIABLES n, pc

vars == << n, pc >>

Init == (* Global variables *)
        /\ n = 0
        /\ pc = "Lbl_1"

Lbl_1 == /\ pc = "Lbl_1"
         /\ n' = n + 1
         /\ pc' = "Done"

Next == Lbl_1
           \/ (* Disjunct to prevent deadlock on termination *)
              (pc = "Done" /\ UNCHANGED vars)

Spec == Init /\ [][Next]_vars

Termination == <>(pc = "Done")

Let’s look at the translation for a moment. We can see that it starts with the definition of the variables, n and pc. The n comes from our pluscal code. But what is this pc?

pc stands for “program counter” and used to track the current execution state of the specification. When the spec is translated, each line is given an implicit label, like “Lbl_1”, “Lbl_2” etc. The value of pc then tracks these labels, with the implicit value “Done” being used to represent the fact that execution has completed.

The rest of the specification is a series of definitions of the form “something == conditions”. One can think of these as mathematical formulas. These formulas are combinations of specifactions using predicate logic. To understand this, let’s start at the bottom, ignoring the definition of Termination for now.

Spec is defined to be Init and the temporal formula Next for the given vars. A temporal formula means that it is true for every behavior or in other words represents the steps in the execution. Init just sets n = 0 and pc = "Lbl_1". We have to remember that this is an assertion and not an assignment as we would normally think of in programming. So we can think of Init as being the state where n and pc have the values as defined.

Next we then see is defined to be either Lbl_1 or we have pc = "Done" and the vars are unchanged. Lbl_1 in turn is a conjunction of asserting that the value of pc = "Lbl_1" and then defining the next value of n and pc, defined by n' and pc' to be n + 1 and "Done" respectively.

So Spec describes all the valid behaviors of this specification represented by the plusCal program above. We now need to check if this specification is correct. We can say that the specification is correct, if after the program completed (the value of pc = "Done"), the value of n = 1.

We can represent this by the definition

AlgoOK == pc = "Done" => n = 1

Remember, in predication logic, F => G (F implies G) means that

• if F is False, then F => G is True
• if F is True, then F => G is True iff G is True.

So this formula is allways True when pc is not equal to "Done" and only true if n = 1 when pc = "Done". Creating an running a model on this specification, with the Invariant set to the formula AlgoOK finds no errors in the specification.

The pretty-printed version of this specification is available here.

Hello Concurrent World

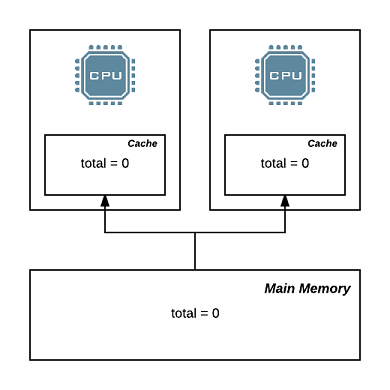
The real power of TLA⁺ though comes across when we start specifying concurrent and distributed systems. Let’s try to model a simple case, namely the behavior of CPU caches and memory. In most modern architectures, there are normally more than one CPU on the motherboard, each with it’s own cache, sharing access to the main memory. The CPU instructions themselves work mostly on data in registered, which are loaded from the caches. In the case of a cache miss, data is fetch from memory on to the cache and then read into the registers for the CPU to work on.

Say we have a variable total that holds an integer value and we have two threads that are trying to increment this variable. This can be visualized like so:

The way TLA⁺ models concurrent behavior in plusCal is with the concept called a process. Each process has it’s own id and can have local state, represented by process specific variables in addition to the global one like n we say in the specification above.

In order to model this with TLA⁺, we first need to define an abstraction in terms of state (variables) and behaviours (steps). We can do so by having the data in main memory be represented by the global variable total. Then we can have up to N processes defined, each representing a thread of execution, and having a local variable x. For each execution, we first read from the global variable to the local variable x, to represent the fetch from main memory to cache, update the local variable by 1, to represent the CPU operation and then update the global variable with the new value of x, to represent the write back from cache to main memory.

The complete algorithm is here. The plusCal code looks as so:

--algorithm RaceCondition
variables total = 0;

process Proc \in 1..N
variable x
begin
 read:  x := total;
  inc:  x := x + 1;
 save:  total := x;
end process;

end algorithm;

where N is a constant that can be defined at model execution time. Unlike in the case of the previous example, we see that each step in the parallel algorithm has been labeled as read, inc and save respectively. We can get the toolbox to autolabel the statement, but manually labeling them gives us an opportunity to say what we mean.

The translation of this comes out to be:

CONSTANT defaultInitValue
VARIABLES total, pc, x

vars == << total, pc, x >>

ProcSet == (1..N)

Init == (* Global variables *)
        /\ total = 0
        (* Process Proc *)
        /\ x = [self \in 1..N |-> defaultInitValue]
        /\ pc = [self \in ProcSet |-> "read"]

read(self) == /\ pc[self] = "read"
              /\ x' = [x EXCEPT ![self] = total]
              /\ pc' = [pc EXCEPT ![self] = "inc"]
              /\ total' = total

inc(self) == /\ pc[self] = "inc"
             /\ x' = [x EXCEPT ![self] = x[self] + 1]
             /\ pc' = [pc EXCEPT ![self] = "save"]
             /\ total' = total

save(self) == /\ pc[self] = "save"
              /\ total' = x[self]
              /\ pc' = [pc EXCEPT ![self] = "Done"]
              /\ x' = x

Proc(self) == read(self) \/ inc(self) \/ save(self)

Next == (\E self \in 1..N: Proc(self))
           \/ (* Disjunct to prevent deadlock on termination *)
              ((\A self \in ProcSet: pc[self] = "Done") /\ UNCHANGED vars)

Spec == Init /\ [][Next]_vars

Termination == <>(\A self \in ProcSet: pc[self] = "Done")

The key difference in this translation is that the program counter pc and the local variable x are defined as an array of values, whose index is the set of number in the range 1..N, or in other words an array of length N starting with 1 (this pascal arrays…). While it is convenient to think of these as arrays, in reality though, they are mathematical functions with the domain set to the range 1..N, but arrays works in practice. In addition the EXCEPT syntax to update the values of array variable at a particular index, while leaving the other’s unchanged.

Similarly, we see the Next formula being defined as “there exists a value called self in the range 1..N such that Proc(self) is True”. Proc(self) in turn is defined to be the disjunction of read(self), inc(self) or save(self). In practice, what this means is that for the next step execution, any valid step on any of the processes could run. Each process in turn can either do a read, inc or save. And what makes a step valid within a process? It’s the precondition check (the first line in each formula). For example, a process can execute it’s read step if the pc value for that process has the value "read".

Now, we come to the validation part of the spec. We can define the invariant formula as follows:

AlgoOK == (\A self \in ProcSet: pc[self] = "Done") => total = N

Or in other words, we say that once all the N processes are done, if the specification is correct, then the value of total = N.

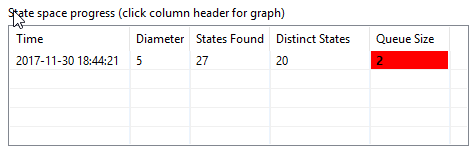
Creating a model with N = 2 (or 2 processes) and running it shows us two important things.

1. The model has 20 distinct states that represent all possible executions of the specifications as follows.

   

2. There exists atleast one possible execution of the specification, where the invariant is violated, as follows:

   

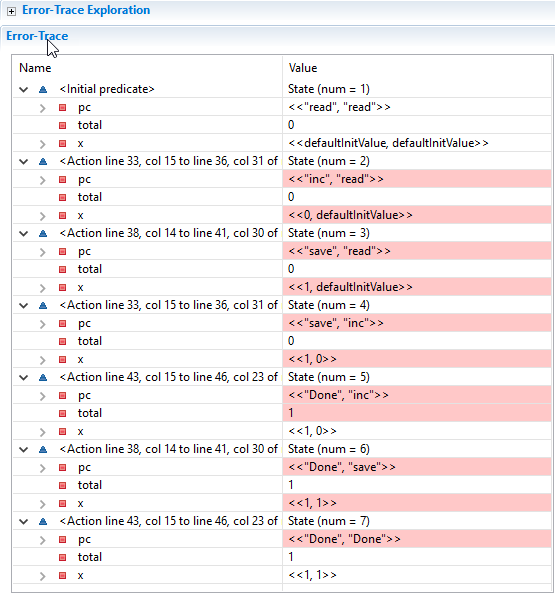
Let’s spend a minute to see what the stack trace says. Translated, it shows the following execution of the specification where the invariant is violated.

1. The specification start with the init state, where the local variable x in each of the process have undefined initial values, and the program counter pc says either process to execute the "read" state.
2. Process 1 runs, and reads the current value of total into x, changing x[1] to 0, and it program counter is updated to the next possible state: pc[1] equals “inc”.
3. Process 1 runs again, and it increments the local value of x, and updates it’s program counter, so: x[1] = 1, pc[1] = “save”.
4. Process 2 now runs and reads the value of total into it’s local variable x, so: x[2] = 0, pc[2] = “inc”.
5. Process 1 now runs again and save’s it’s local value to total, and updates it’s program counter to “Done”, so: total = 1, pc[1] = “Done”.
6. Process 2 now runs and increments it’s local variable x, and updates it’s program counter, so: x[2] = 1, pc[2] = “save”.
7. Process 2 now save’s it’s local value to total, and updates it’s program counter to “Done”, so: total = 1, pc[2] = “Done”.

Here we see that as per the specification, if the second process happens to read the value of total before the first process has completed it’s update, it reads a stale value and over-writes other updates with it’s own computation when it is done, which then breaks the invariant that says that at the end of the specification, we should have total = N or total = 2 in this case.

Or in other words, un-synchronized access to shared memory leads to heisenbugs. Why heisenbug? Because the model does not say that this execution will always happen. But rather, as per the specification, and all it’s allowed behaviour, there is one possible execution, which, if it happens, breaks the invariant that shows that the specification is correct. To restate it, the design/specification has a flaw and is broken!.

So how do we fix it?

What we need to do is to synchronize the access to total so that only one process (or thread in practice) can acess and update it at any given time. The way we can do this in plusCal is using the await statement which says, only execute the next statement, if the current condition under await is True.

We can then use an ordinary variable, let’s call it have_lock and have each process first await have_lock = FALSE or in other words, check that no other process has taken a lock, and atomically set have_lock := TRUE once this condition passes for a given process i, so that no other process can then take the lock. At the end of the update, we release the lock by setting have_lock := FALSE, so that some other process can now take the lock.

To make the process of locking and unlocking stand out, we write these as macros which are then replaced at the caller site during the translation. Putting all this together, the specification evolves to:

--algorithm RaceConditionLock
variables total = 0, have_lock = FALSE;

macro Lock()
begin
    await have_lock = FALSE;
    have_lock := TRUE;
end macro;

macro Unlock()
begin
    have_lock := FALSE;
end macro;

process Proc \in 1..N
variable x
begin
  lock: Lock();
  read: x := total;
   inc: x := x + 1;
  save: total := x;
unlock: Unlock();
end process;

end algorithm;

The complete code is here. Translating this yeilds:

CONSTANT defaultInitValue
VARIABLES total, have_lock, pc, x

vars == << total, have_lock, pc, x >>

ProcSet == (1..N)

Init == (* Global variables *)
        /\ total = 0
        /\ have_lock = FALSE
        (* Process Proc *)
        /\ x = [self \in 1..N |-> defaultInitValue]
        /\ pc = [self \in ProcSet |-> "lock"]

lock(self) == /\ pc[self] = "lock"
              /\ have_lock = FALSE
              /\ have_lock' = TRUE
              /\ pc' = [pc EXCEPT ![self] = "read"]
              /\ UNCHANGED << total, x >>

read(self) == /\ pc[self] = "read"
              /\ x' = [x EXCEPT ![self] = total]
              /\ pc' = [pc EXCEPT ![self] = "inc"]
              /\ UNCHANGED << total, have_lock >>

inc(self) == /\ pc[self] = "inc"
             /\ x' = [x EXCEPT ![self] = x[self] + 1]
             /\ pc' = [pc EXCEPT ![self] = "save"]
             /\ UNCHANGED << total, have_lock >>

save(self) == /\ pc[self] = "save"
              /\ total' = x[self]
              /\ pc' = [pc EXCEPT ![self] = "unlock"]
              /\ UNCHANGED << have_lock, x >>

unlock(self) == /\ pc[self] = "unlock"
                /\ have_lock' = FALSE
                /\ pc' = [pc EXCEPT ![self] = "Done"]
                /\ UNCHANGED << total, x >>

Proc(self) == lock(self) \/ read(self) \/ inc(self) \/ save(self)
                 \/ unlock(self)

Next == (\E self \in 1..N: Proc(self))
           \/ (* Disjunct to prevent deadlock on termination *)
              ((\A self \in ProcSet: pc[self] = "Done") /\ UNCHANGED vars)

Spec == Init /\ [][Next]_vars

Termination == <>(\A self \in ProcSet: pc[self] = "Done")

The differences we see here, is that, in addition to read(self), inc(self), save(self) from before, we also have lock(self) and unlock(self) as valid steps for given Proc(self). The await have_lock = FALSE; have_lock := TRUE get’s transalated as the precondition have_lock = FALSE in conjunction with the update have_lock' = FALSE within the lock(self) definition.

Since when a given definition is evaluated, all it’s sub-formula’s have to evaluate to true, if a given process successfully executes the lock step, no other process can take the lock as the precondition have_lock = FALSE will fail till the process that took the lock executes the unlock step.

The invariant definition AlgoOK stays same as before.

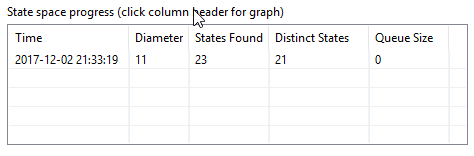
Creating a running a model on this updated specifation, with N = 2, now shows that there are 21 distinct states and No Errors as follows:

The pretty-printed version of the specification as originally specified, and then updated with the lock are available here and here.

Practical Considerations

Ordering of memory reads and writes, and then sychronization across different processers within a program is normally performed using memory barriers. These get exposed in different forms in various programing languages.

For example, see the following presentation on the Java Memory Model and how the memory ordering is guaranteed (or not) by the JVM under various conditions.

So while we can reason about and prove that a given specification is correct using TLA⁺, translating into code will still need to consider implementation specific concerns, like the Java Memory Model to ensure that the it adheres to the specification as defined!